Maximizing Homeschool Math

by Steve Leinwand and Caroline Welty

Preparing kids to be able to apply mathematics in relevant, current contexts – full of data, technology, and wide-reaching demands for quantitative literacy – goes far beyond merely teaching and practicing rote skills, and this goes for classroom teachers and homeschooling parents alike. It’s not enough to tell, show, and drill math skills when working to develop mathematical skills and conceptual understanding that result in the number sense, spatial sense, symbol sense, and data sense needed to confidently solve math problems relevant to today. To achieve these goals for our children, we believe that there is a set of non-negotiable, high-leverage practices for teaching math in homeschooling environments.

Years ago, Steve marveled at how 15 one-hour tutoring sessions allowed him to address more than he ever could in 180 50-minute Algebra 1 classes. Quick math – that’s comparing 15 hours to 150 hours, making the tutoring sessions ten times more effective than traditional classes. He didn’t just cover the math, but he was also able to teach it with far more understanding and achievement. More recently, Caroline experienced how weekly 45-minute tutoring sessions with struggling middle schoolers improve self-confidence, elevate attitudes toward math, and raise achievement. When we (Steve and Caroline) compared notes as grandfather and granddaughter, we were struck by the overlap in our approach and the way we both attributed our success to specific practices. Here are five accessible and research-affirmed practices that we believe undergird effective math teaching in homeschooling contexts.

Strategy #1: Clearly identify your homeschoolers’ strengths and needs to drive instruction.

We believe that everyone can be a mathematician, but different students learn math in different ways. Some students need to see the math with symbols and pictures. Others learn better through listening, while others need both sensory modes to understand concepts. Others learn best with real-world contexts and applications, while some need to touch and manipulate objects to solidify understanding. To further complicate things, students bring different strengths to different parts of mathematics. For example, drawing pictures is often essential for learning geometry, while tables and graphs support the learning of algebraic equations and functions. When instruction overlooks the individual needs of some students or fails to draw on their strengths, learning can get very frustrating. Matching our approaches to learners’ strengths and needs is a powerful component of effective instruction. Here’s an example:

Pay attention to students’ thinking processes. Assessment isn’t merely reviewing students’ answers – it’s looking at their thinking that provides you with the richest information. That is why we encourage students to think aloud while we work through problems together or when they’re working on their own. Independent work is important, but when a student does independent work, try to balance it with working together to see and hear how they solve problems, not just if they can arrive at the correct answer.
Ask yourself four questions:
- What do they know?
- What do they struggle with?
- What gaps do they have?
- How do they best process the math and visualize the math they are learning?

For example, if a student struggles with subtracting and regrouping, combine broad observation and more focused diagnosis to determine if issues stem from misunderstanding place value, lacking subtraction facts, or both. If a weakness doesn’t immediately appear and students are still struggling, keep looking.

Strategy #2: Carefully plan your math lessons.

Too many of us have a typical, but lacking, understanding of a math lesson – start with an example and explain how to get the correct answer, work together on a second (very similar) problem, and then provide a set of similar problems for practice, with a focus on getting the most problems correct in the shortest amount of time. Here are two examples – a detailed lesson plan versus an example of scaffolded tasks that provide alternative approaches to lesson planning.

Here is a sample lesson plan that identifies a set of lesson chunks with clarifying examples of each chunk.

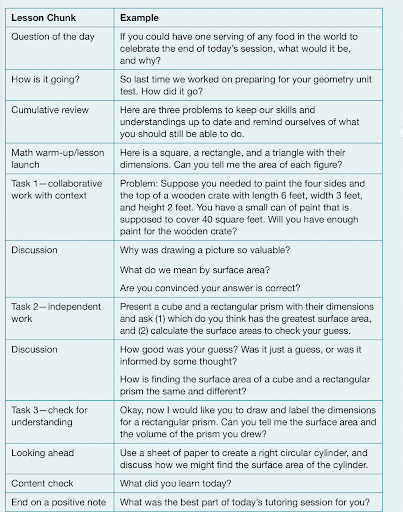
Give learners a sequence of scaffolded problems or tasks that allow them to see how mathematical skills and ideas build from what they already know. For example, one of us recently observed a lesson on multiplying mixed numbers by whole numbers. We could teach this in traditional rule-driven ways by just telling students to change the mixed number to an improper fraction and put the whole number over 1 and then treat the problem as any multiplication of fractions problem. Or the teacher carefully scaffolded the problem, beginning with asking students to multiply 32 x 21 in two different ways. It was wonderful to see students on their personal white boards use the standard algorithm while others used the partial products alternative algorithm, and still others drew a rectangle and decomposed 32 into 30 and 2 for the length and then 21 into 20 and 1 for the width. In all cases, traditionally, alternatively and with a picture, students got an answer of 672 and were reminded of the value of decomposing numbers.
Next, students worked on ¾ x 8 (also review), but allowed the teacher to focus on decomposing the ¾ into 3 x ¼. Some students then saw that they could multiply 3 by 8 and then divide the 24 by 4, while others divided the 8 by 4 and then multiplied the 2 by 3. Yes, this took time, but when the teacher finally presented the problem 1 ¾ x 16, students were able to dig in with confidence. They learned that multiplying mixed numbers by whole numbers was not a completely new skill, but a skill that builds directly on prior knowledge.

Strategy #3: The heart of effective tutoring is in the questions we ask.

As homeschooling instructors, we learn far more about our students and their learning processes (and our students learn far more about math) when we ask questions and wait for answers, rather than from merely talking and showing. For example:

As tutors, we always hear ourselves asking questions like:
- Why?
- Can you convince me?
- Did your brain picture that situation?
- Can you explain that to me

Ask these questions frequently after receiving both correct and incorrect answers. This helps learners think and reason that supports real learning and understanding.

When we plan our tutoring sessions, we pay as much attention to the questions we intend to ask as we do to the tasks we present. Questions like “Why did you multiply instead of divide?” or “How would you convert centimeters to meters?” help us focus on key understandings.

Strategy #4: Focus on alternative approaches and multiple representations.

Students process mathematics differently, therefore visualizing mathematics in different ways. There are no one-size-fits-all approaches. In fact, one of the most common reasons that students struggle with mathematics, and can benefit greatly from tutoring, is that their brains see and make sense of the math in nontraditional ways, requiring us to consistently suggest different approaches and different ways of visualizing the math they are learning in an ongoing search for the approach that clicks. For example:

Consider a student struggling to remember the sum of 8 and 9. Many times it seems that all the practice in the world doesn’t seem to cement this fact into memory. Perhaps it’s time to recognize that the neural connections that link 8 and 9 to 17 just aren’t there and can’t be coaxed into existence. Our approach is to ask how else might this student retain or derive this fact. We talk about and model doubles plus one (8 + 8 + 1 = 16 + 1 = 17) or we discuss replacing 9s with 10 and then subtracting one (8 + 9 = 8 + 10 – 1 = 18 – 1) or using tens frames to visualize 8 + 9 as 10 plus 10 – 2 – 3).

Consider the middle or high school students struggling with adding and subtracting signed numbers such as finding 5 + (-9). Instead of memorized rules that make little sense to most students, we turn to football plays and ask students to visualize gaining 5 yards on the first play and then losing 9 yards on the second play to picture how losing 5 takes you back to the start and yet you have 4 more yards back to go to get to -4. Or remember that for some students the horizontal number line is not a friend and their brain sees up and down better than left and right. For these students we turn to above and below sea level, or thermometers or elevators and connect signed numbers. Sometimes it’s a simple matter of helping learners consider starting with $5, but owing his or her mother $9 to see that 5 + (-9) must equal -4.

Honor and use mistakes as learning opportunities.

An essential mindset for effective math teaching is that mistakes are part of the learning process. In fact, mistakes are windows into understanding and misunderstanding and therefore provide critical insights into building understanding. Renowned mathematics educator Jo Boaler has summarized a mountain of neurological research and argues that mistakes actually “grow one’s brain” and support both teaching and learning when they are properly addressed. Contrast that with typical and deflating responses that many students receive upon making a mistake: “No!” “Wrong!” “Try it again and get it right this time.” Here are two approaches to maximizing the conversion of mistakes into deeper understanding:

As noted above, it is important to clearly communicate to learners that you love to see their mistakes and you try to practice using a big smile when you comment, “Almost, let’s see if together we can find your mistake.” Similarly, you have a responsibility to make it clear that, unlike how you were probably taught math, focusing on right answers and the one right way to solve a problem may help in the short term, but fail to support the kind of long-term understanding that constitutes enduring mathematical know-how.
Since students often learn that we only ask them questions when they are wrong, consider practicing asking “Why is that?” or “Can you explain?” just as often when you get a correct answer as when you get a mistake. This deemphasizes the negative connotation of mistakes, gives students a chance to think and explain all of their answers, and provides you as the teacher with lots of evidence about where the mistake or misunderstanding emerges.

Looking for more tips and ideas for effective mathematics instruction? Check out our book, The Math Tutor’s Handbook: Strategies and Tips for Success, published by Corwin.

Through a range of activities, checklists, examples, stories, and suggestions, this PreK-12 handbook:

Focuses on the importance of personalized instruction that no computer program can match
Describes how to develop strong, supportive relationships between tutor and student
Identifies common stumbling blocks around the big ideas in mathematics across grade levels and suggests how to overcome them
Celebrates mistakes as valuable learning opportunities to foster a deeper comprehension of mathematical concepts rather than just getting the right answer
Promotes skills needed for the future, such as problem-solving and critical thinking, which are beneficial not only in future math classes but also in various aspects of life and work

Use this handbook to help you create a positive learning environment for your learners, boost their self-confidence, reduce math anxiety, and master essential skills. Whether you are a private tutor or parent, you work in a tutoring center, or you are an in-school K-12 math teacher, coach, or specialist, this is the resource you need for the math tutoring strategies and practices that are foundational to successful learning.

Steve Leinwand is an award-winning K-12 mathematics consultant, author, speaker, change agent and critical friend who spent 10 years in the classroom, 20 years as Supervisor of Mathematics in the Connecticut State Department of Education and 20 years as a Principal Researcher at the American Institutes for Research. He is a past president of the National Council of Supervisors of Mathematics.

Caroline Welty is a high school senior in North Carolina and a much sought-after tutor of upper elementary and middle school students. She is an award-winning debater and an accomplished vocalist who was recently selected for the prestigious State of North Caroline Honors High School Chorus. She hopes to become a teacher and eventually an educational policy-maker to improve the current system of schooling to better serve all students.